Keith Schwarz (htiek@cs.stanford.edu)
Recursion to the Rescue! is a trio of recursive backtracking problems designed to give recursion "stakes" by solving problems related to health care, public policy, and politics. Students solve classic NP-hard optimization problems and see applications to hospital scheduling, disaster preparedness, and US Presidential Elections.
There are three pieces to this assignment, which could be used individually or mixed and matched into a single assignment:
This assignment is somewhat challenging, but the payoff for students after finishing is enormous. I've used these assignments several times and at the end of the quarter students routinely rate these problems as the most rewarding parts of the course, both due to the satisfaction of getting them working and their inherent interest in the application domain (public health and safety, US politics).
For students who go onward to take future courses in topics like algorithms or NP-hardness, this assignment has the additional benefit of reframing classic but abstract NP-hard problems (dominating set, bin packing, and knapsack, respectively) in ways that make them seem much more tangible. Students often ask whether they can speed up their disaster planning program or why we don't use the Doctors Without Orders program for broader healthcare questions. Giving an answer of the form "no one knows whether we can markedly improve upon the algorithms you're coding up right now, and you can take more CS to learn why" is a great way to bridge the Theoryland/coding divide.
| Summary | Students write three recursive backtracking problems that give insights into hospital scheduling, US elections, and disaster preparations. |
| Topics | Recursive backtracking, maps, sets, and lists. |
| Audience | This assignment is designed for a CS2 course. |
| Difficulty | This is a challenging assignment. We usually give students one-and-a-half or two weeks to complete all three parts, with our "honors" course sometimes dialing that down to only one week. Students usually report that the payoff at the end makes it worth it. |
| Strengths | From a coding perspective, the assignment exercises three different flavors of backtracking recursive searches (searching over assignments, searching over subsets in a traditional include/exclude pattern, and searching over subsets in a problem-specific way). From a Theoryland perspective, this assignment exposes students to three classic NP-hard optimization problems. And from a social impact perspective, this assignment gives students a sense of the sorts of policy questions that we can approach through a computational lens. |
| Weaknesses | It can be tricky for students to test their solutions, partially because recursive backtracking is hard to debug in the first place and partially because writing good test cases here is nontrivial. This latter aspect could be offset by introducing more test cases into the starter files, or perhaps by rewarding students for designing good test cases. |
| Dependencies | This assignment assumes knowledge of recursive backtracking and standard data types like maps, sets, and lists. Although this assignment was given out in a course taught in C++ that uses custom C++ libraries, it would not be difficult to adapt this assignment to work in other languages like Python, Java, etc.; the core algorithms just use basic containers and the visualizations shouldn't be too hard to port to other platforms. |
| Variants | Students have found all sorts of ways to modify this assignment. Choosing the most constrained city at each point in time in the Disaster Planning problem dramatically boosts performance. Requiring patients to be seen by doctors with different specialties leads to a more interesting and challenging problem. Making assumptions about how various states might or might not vote produces a program that lets students explore different election forecasts. |
Here's a quick rundown of each part of the assignment.


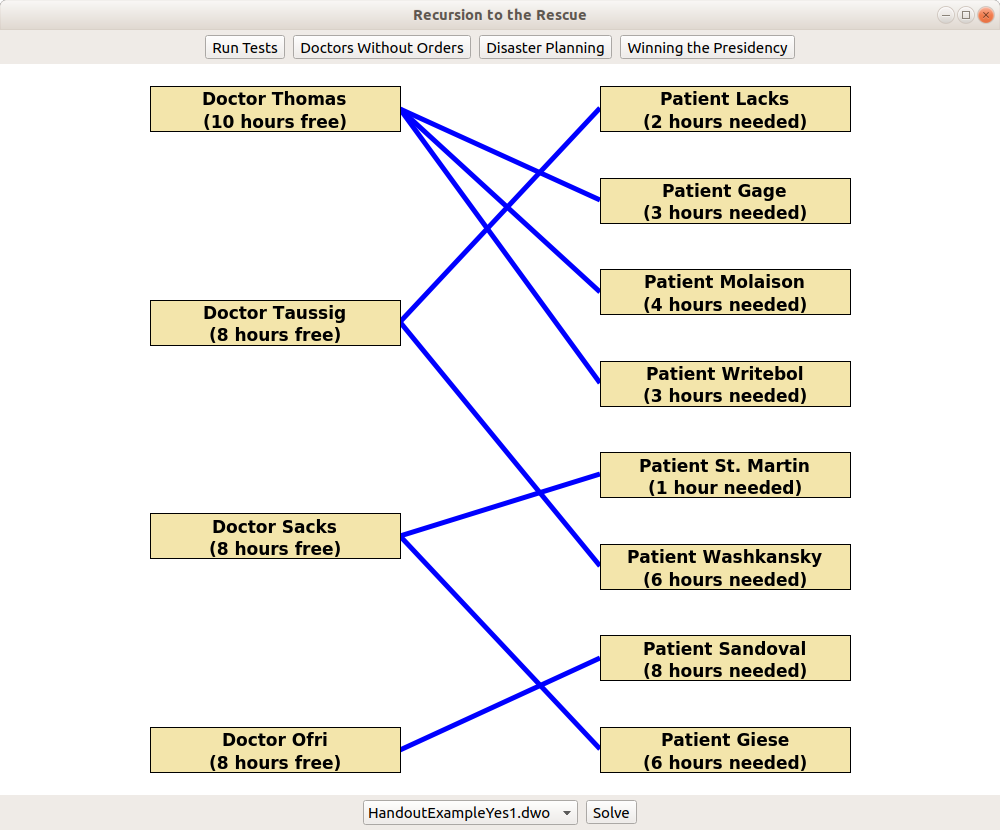
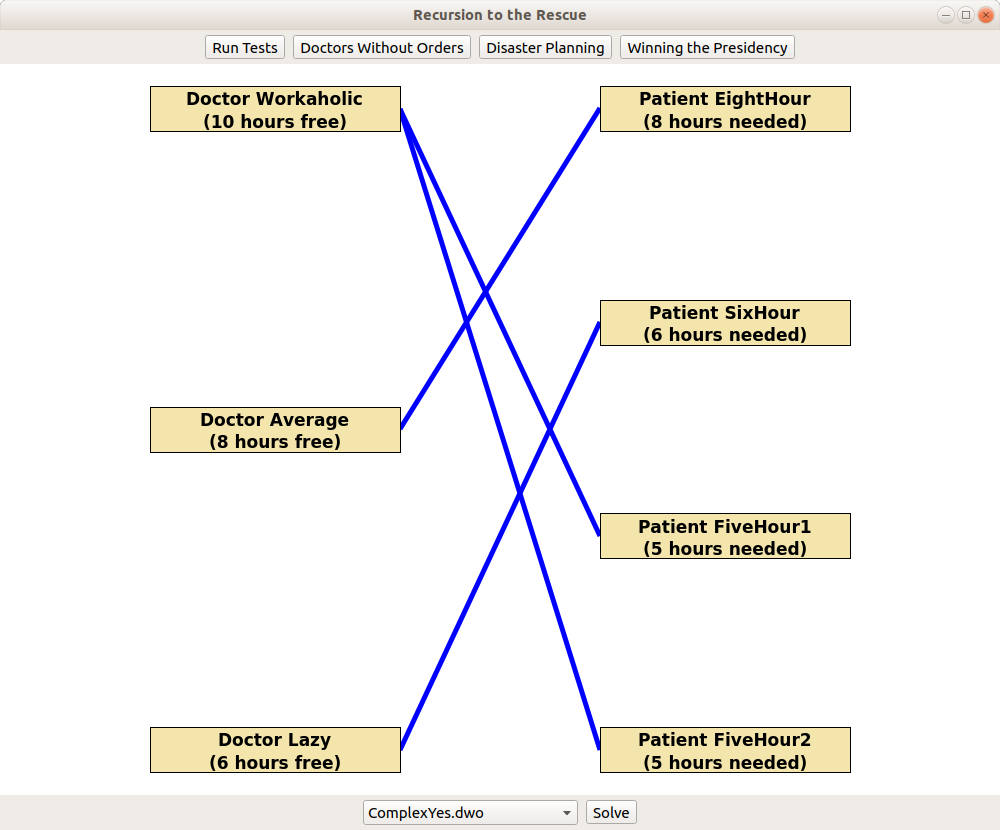
In this problem, students are given a list of doctors and a list of patients. Each doctor only has so many free hours available, and each patient requires a certain amount of time to be seen. Can you schedule each patient so that they're seen, and, if so, how?
The backtracking in this part of the assignment requires students to explore different assignments of patients to doctors. Students have to first figure out how to enumerate all possible solutions (the key insight being that it's easier to pick an unscheduled patient and schedule them than to pick an unassigned doctor and pack their schedule), then convert that into a working backtracking recursion.
The starter files contain a number of sample doctor/patient sets and a visualizer that shows the assignment of doctors to patients that the student produces (or reports that no possible assignment can be made, if that's the case).
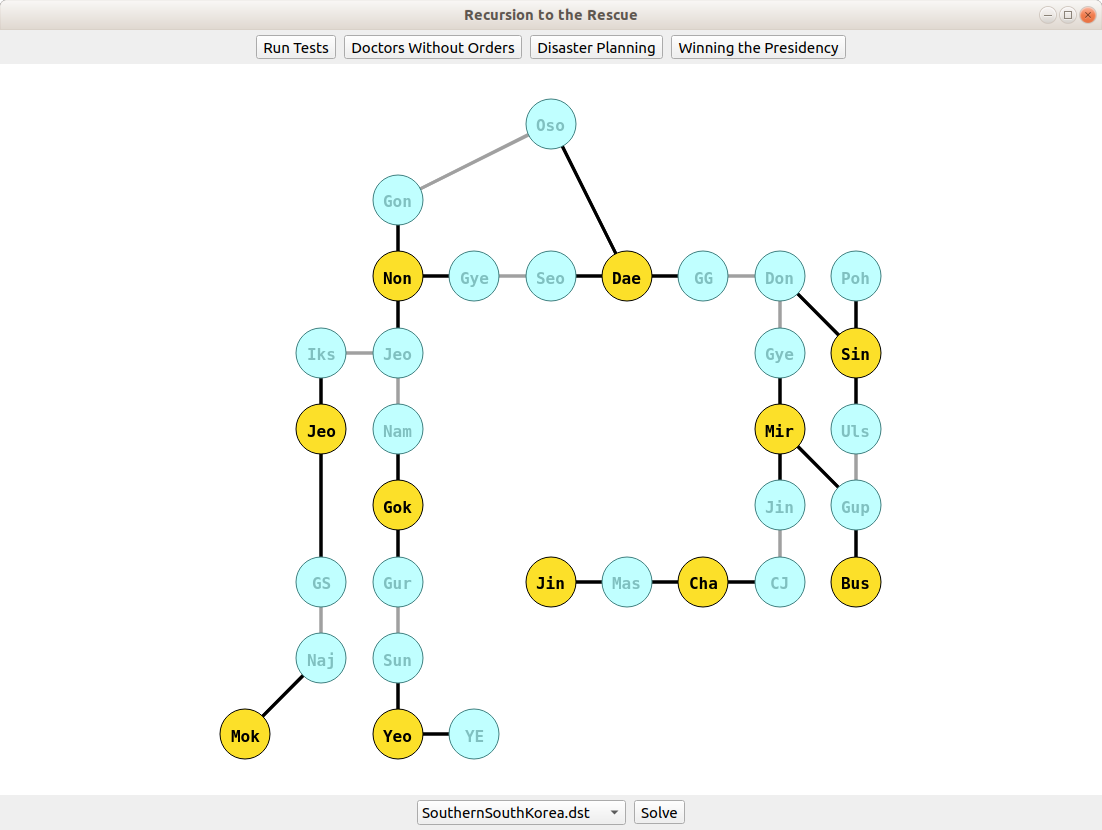
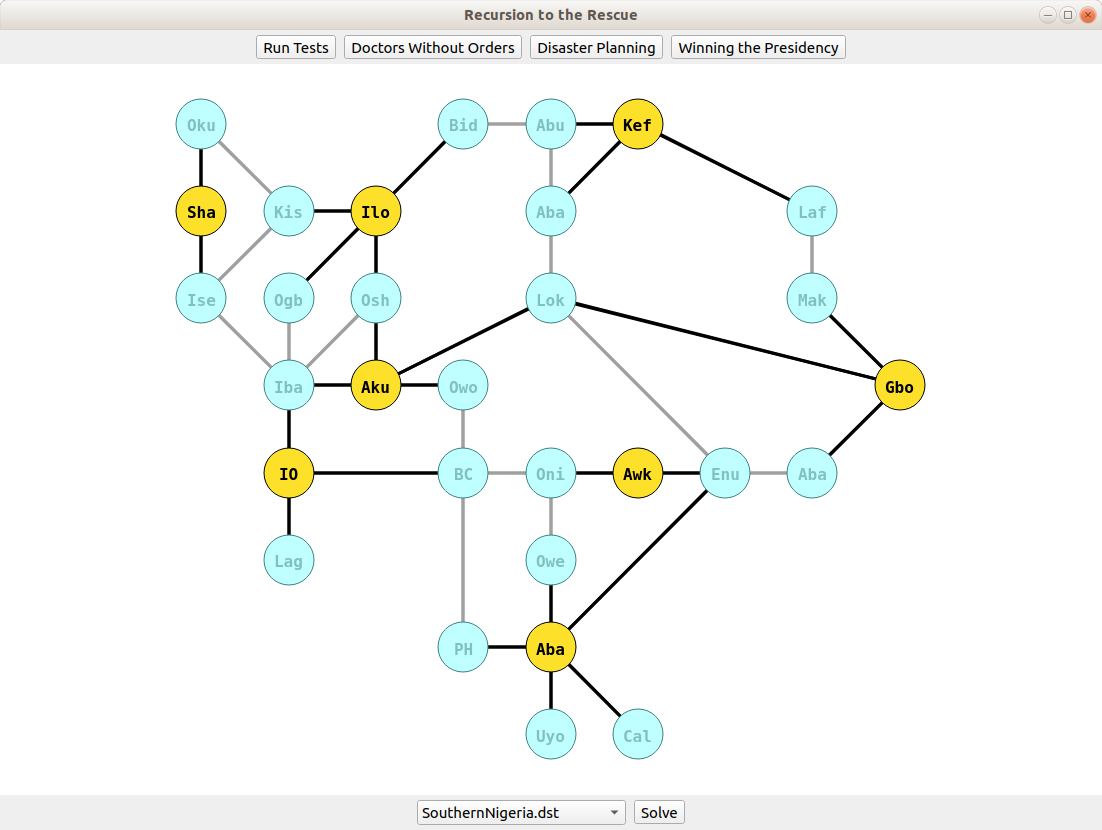
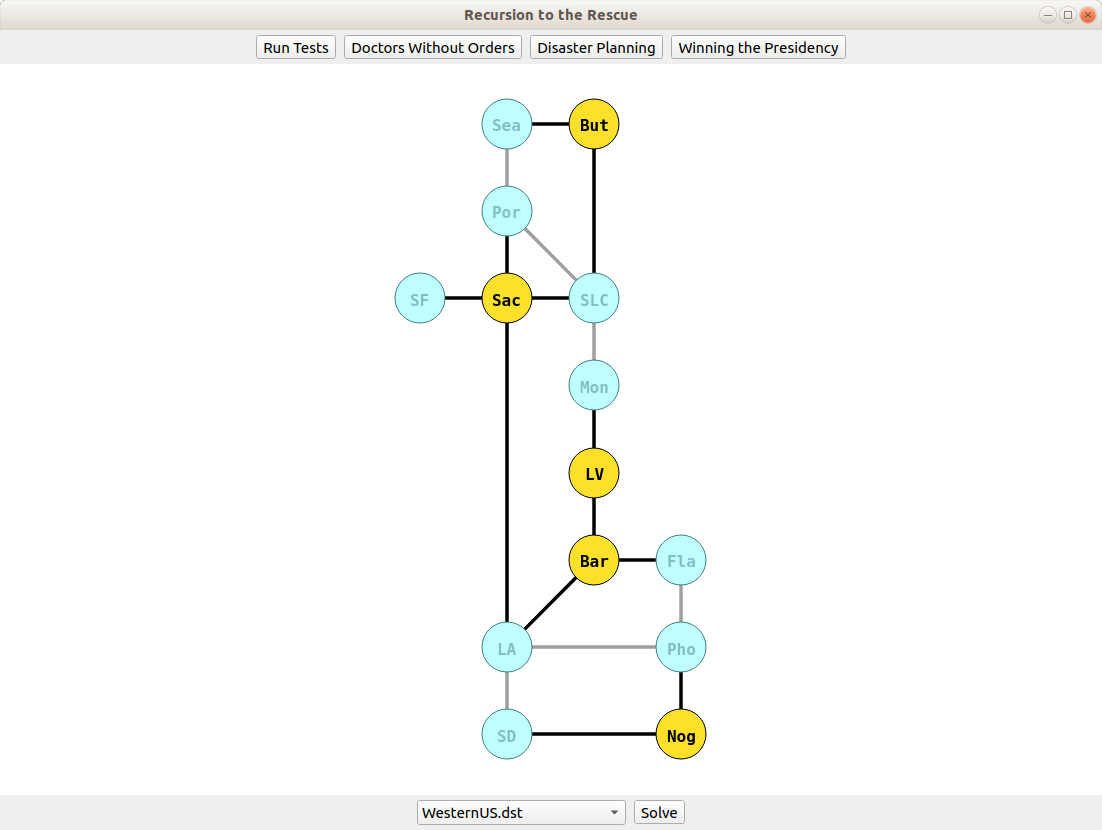
You have the transportation grid for a region represented as a map from cities to their neighbors. You have the budget to stockpile emergency supplies in only so many cities. Can you feasibly stockpile supplies so that each city either (1) has supplies or (2) is adjacent to a city that does?
Our suggested algorithm - which runs pretty fast in practice - is to pick a city arbitrarily, then recursively explore all ways of providing coverage to it (either by covering it, or covering one of its neighbors). If any of those choices lead to success, great! You can provide coverage. If not, then coverage can't be provided.
The assignment starter files visualize various transportation networks and use a binary search with the student's function to find the smallest set of cities providing coverage. These data files are based on major transportation lines in different regions (highways, rail lines, etc.).
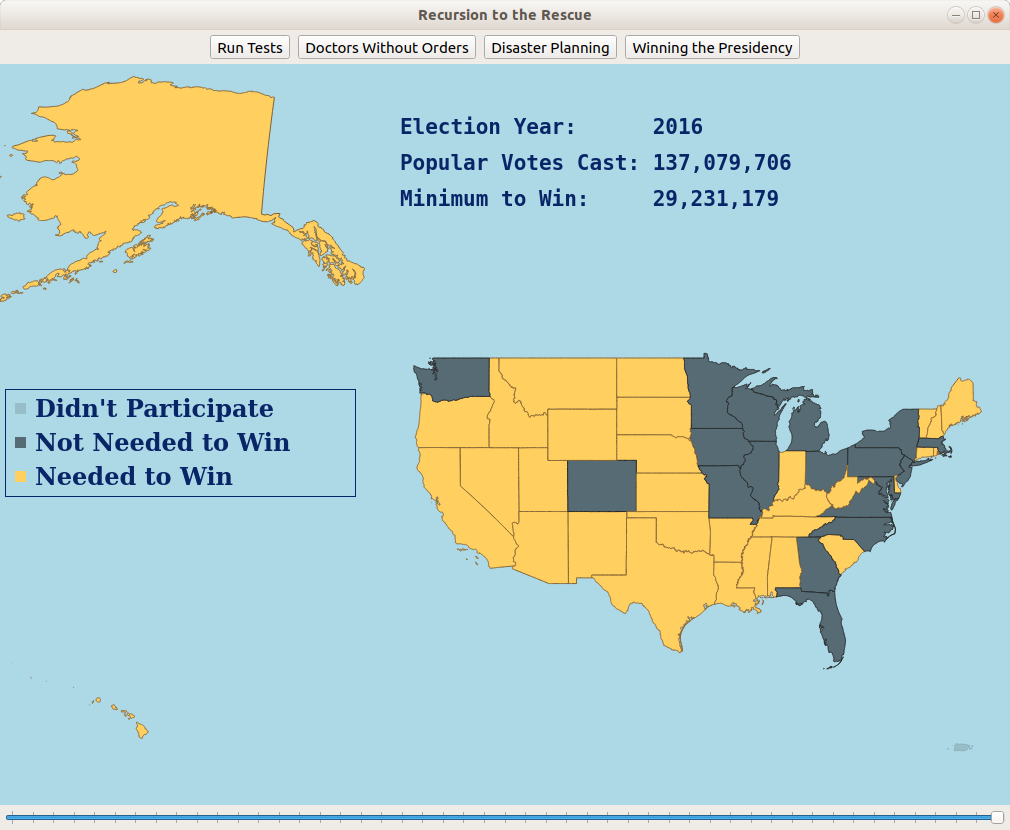
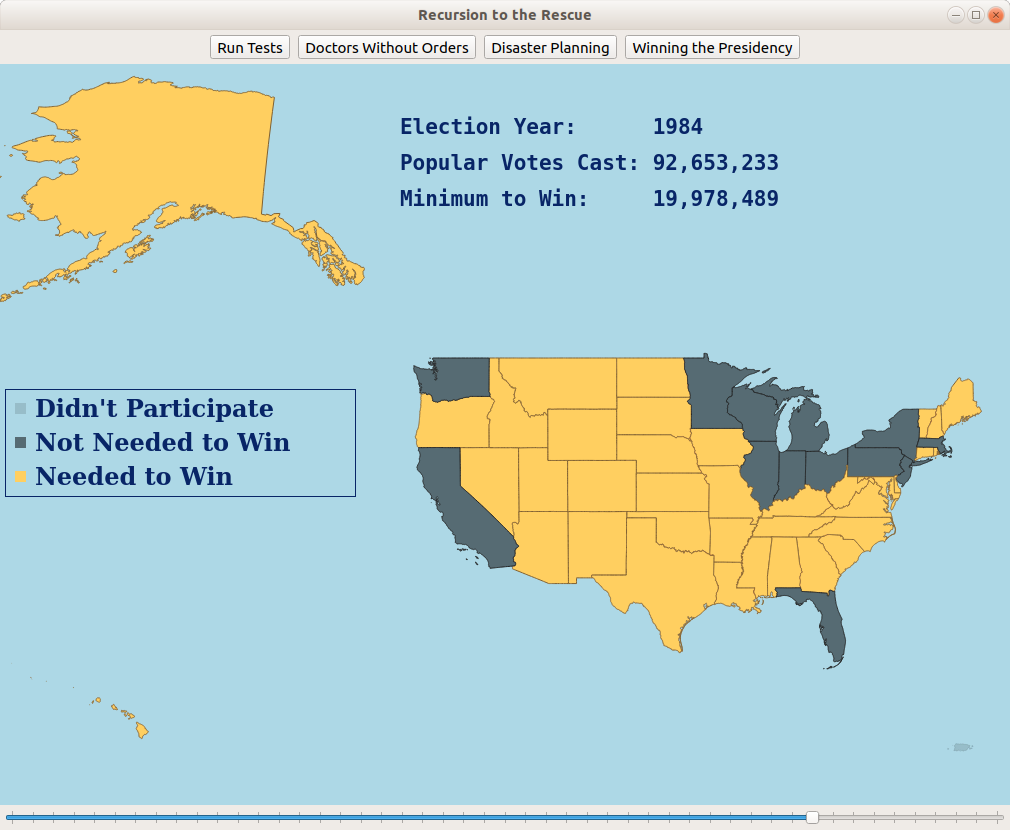
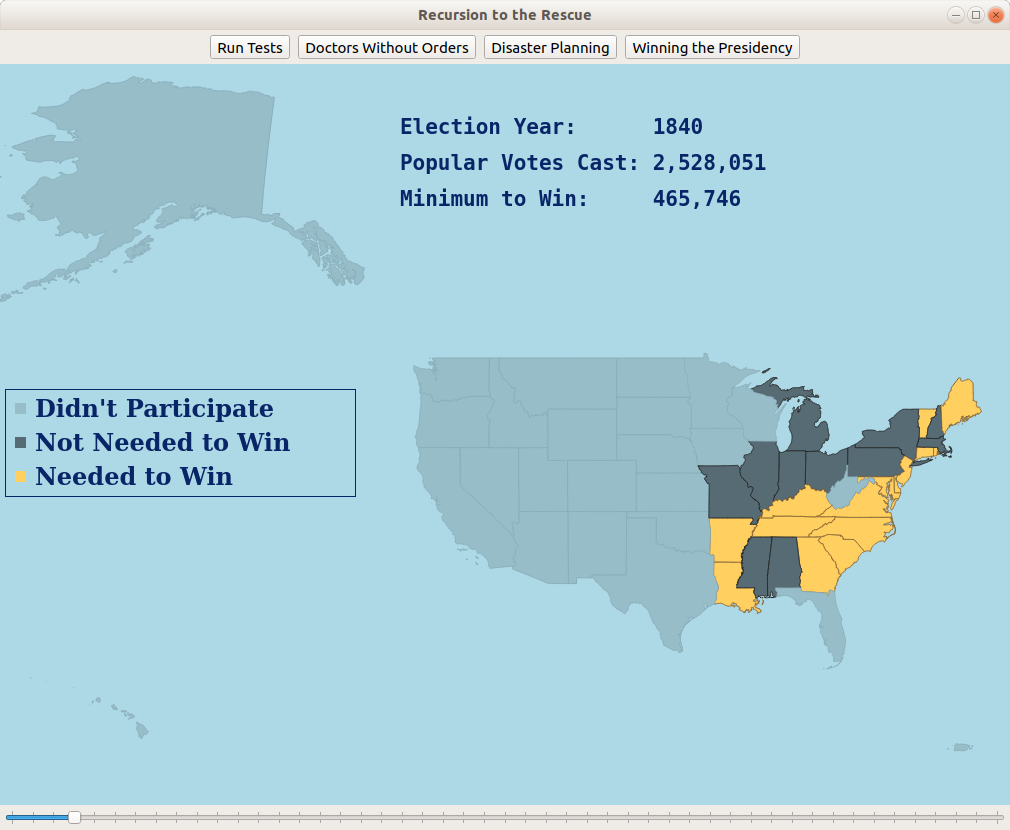
Given how many people voted in each state in an election and how many electoral votes each state has, how few votes can you get and still get elected President? And which states would you carry in the process?
You might recognize this as the knapsack problem! Each state has a "weight" (number of popular votes) and a "value" (number of electoral votes). The goal is to then minimize the weight that reaches a certain value. Using memoization or dynamic programming, it's possible to very quickly solve this knapsack instance.
This section of the assignment comes with a visualizer with historical voting records for US Presidential Elections going back to the 1820s. The student can adjust a slider bar to change the year, seeing how few popular votes would be needed and what the winning voting coalition would look like.