A hammered dulcimer is percussion instrument with rows of strings, stretched out over a trapezoidal base. A musician plays the instrument by striking the strings with small mallets, or hammer.

Note that in each dulcimer shown above, there are two internal bridges that hold up the strings. The bridge on the right is known as the bass bridge and the strings to the right of it are the bass strings. The bridge to the left is known as the treble bridge, and the strings to the left and right of it are the treble1 and treble2 strings, respectively. The strings can be tuned to different patterns, but the most common arrangement is shown below (where '+' after a note denotes a higher octave and '-' denotes a lower octave):

The physics behind stringed instruments is rather interesting. When a dulcimer string is struck by a hammer, the string vibrates and creates sound. The vibration can be measured by sampling the displacement of the string at equally spaced points. These displacement measurements can be stored digitally, say in a list or queue structure, then used to recreate the sound wave over a speaker.

For this assignment, you will store the displacement values for a dulcimer string in a queue structure. When at rest, the string can contain energy at any frequency. This is modeled by assigning the queue to contain random real numbers between -1/2 and +1/2. After the string is struck, it vibrates causing a displacement that spreads wave-like over time. The Karplus-Strong algorithm simulates this vibration using a fairly simple update process: it repeatedly adds to the end of the queue the average of the first two samples, scaled by an energy decay factor of 0.996, and removes the first sample from the queue.

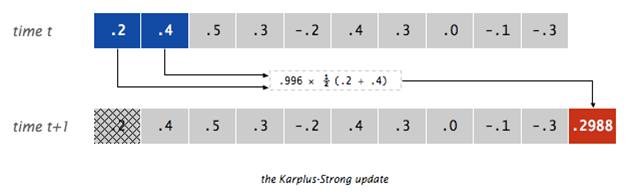
This simple algorithm provides an effective model of the string vibration due to two features: the queue feedback mechanism and the averaging operation.

1. The queue feedback mechanism. The queue models the medium (a string fixed at both ends) in which the energy travels back and forth. The length of the queue determines the fundamental frequency of the resulting sound. Sonically, the feedback mechanism reinforces only the fundamental frequency and its harmonics (frequencies at integer multiples of the fundamental). The energy decay factor (.996 in this case) models the slight dissipation in energy as the wave makes a roundtrip through the string.
2. The averaging operation. The averaging operation serves as a gentle low pass filter (which removes higher frequencies while allowing lower frequencies to pass). Because it is in the path of the feedback, this has the effect of gradually attenuating the higher harmonics while keeping the lower ones, which corresponds closely with how a struck wire actually sounds.

Part 1: Modeling a dulcimer string

For the first part of this assignment, you are to implement a class that models a single dulcimer string. Your DulcimerString class should provide the following constructor and methods:

public DulcimerString(String note)

The class constructor takes a single input, a String representing a note. The 12 notes in the chromatic scale are represented by "A", "A#", "B", "C", "C#", "D", "D#", "E", "F", "F#", "G", and "G#". Plus and minus signs can be added to the end of a note to specify a higher or lower octave. For example, "C+" is high-C (one octave or 12 notes above middle-C), whereas "G-" is low-G (5 notes below middle-C).

The constructor should initialize a queue containing N zeros, where N is the nearest integer to:

        SAMPLE_RATE * 2(22 - offsetFromMiddleC)/12 / 440

Here, SAMPLE_RATE is a constant defined in the StdAudio class, which was developed at Princeton. See below for details on calculating a note's offset from middle-C.

public String getNote()

This method returns the String representing the note, e.g., "C", "D#+".

public int getOffsetFromMiddleC()

This method returns the offset of the note from middle-C, i.e., how many notes up or down it is in the chromatic scale. For example, C-sharp ("C#") is one note higher than middle-C ("C"), so its offset is 1. Low-G is 5 notes lower in the scale, so its offset is -5.

One approach to calculating the offset is the following:

1. Create a list that contains the notes in the chromatic scale ("A", "A#", ..., "G#").
2. Remove any '+'/'-' characters from the note, and find its index in the scale list. For example, given "D+", remove the '+' and determine that "D" occurs in index 5.
3. Subtract 3 from the index to account for the fact that "C" is not the first note in the scale. As a result, the offset for "D" is 5-3 = 2.
4. Finally, adjust for the '+'/'-' characters that were removed. Add 12 (the number of notes in the scale) to the index for each '+'. Alternatively, subtract 12 from the index for every '-'. Here, "D+" contained one '+', so its offset if 2+12 = 14.

public void strike()

This method simulates striking the string with a hammer, by replacing all of the values in the queue with random values from the range -0.5 to 0.5. The size of the queue should remain unchanged.

public double sample()

This method returns the value currently stored at the front of the queue. It also updates the contents of the queue so that a different sample is obtained each time the method is called. The update adds a new value to the rear, which is the average of the two front values multiplied by a decay factor of 0.996, and removes the value from the front. See the diagram above for an example of this update operation.

You should test your class thoroughly by creating dulcimer strings and inspecting their contents after each update. Once you are convinced that the class is behaving as desired, you may integrate it with the provided Dulcimer and DulcimerDriver classes. The Dulcimer class is a working (but incomplete) implementation of a virtual dulcimer, with only the bass strings represented. The DulcimerDriver class allows you to play the bass strings by hitting keys on the keyboard.

The routines for rendering the vibrations using your computer's sound card are contained in the utility class StdAudio. The routines for processing keyboard events are contained in the utility class StdDraw, which was also developed at Princeton.

Part 2: Extending the dulcimer model

Currently, the dulcimer can only play the bass strings. You are to modify your Dulcimer and DulcimerDriver classes so that all three rows of strings are represented and playable. The treble1 strings should be played using the keys on the top row of the keyboard ("1234567890-="), while the treble2 keys should be played with the next row of keys ("qwertyuiop[]").

As part of your modifications, you should add text to the display window that informs the user of the key mappings for the treble strings.