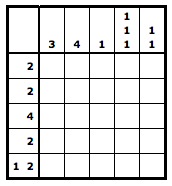
For this assignment, you are to design and implement a Java program for solving Nonogrid puzzles. Nonogrids are Japanese logic puzzles played on a square grid. Each spot on the grid can be either blank or filled, and constraints are provided for each row and column in the grid. For example, the image on the left shows an empty 5x5 grid.


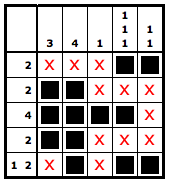
To the left of the rows are sequences of numbers, describing the pattern that filled spots in the rows must follow. For example, the first row has a single constraint, "2", signifying that there must be one contiguous sequence of two filled spots in the row. The last row has a two number constraint, "1 3", signifying that there must be two contiguous sequences of filled spots, of length 1 and 3, with at least one blank spot separating them. Similarly, each column has constraints that describe the pattern of filled spots in that column. To complete a Nonogrid puzzle, the player must fill in spots so that all row and column constraints are met. The image on the right shows the solved puzzle, with black squares in the filled spots and red X's in the blank spots.
For the first part of the assignment, you are to implement a class named Nonogrid that represents a Nonogrid puzzle. The constructor for the class should take a filename as parameter, and read the puzzle information from that file. The first line in a puzzle file will be the number of rows and columns in the puzzle, followed by the column constraints, then the row constraints (one line of text per column/row). For example, a text file representing the above Nonogrid would appear as follows:
Your Nonogrid class should have methods named markSpot and eraseSpot for manually setting the contents of a particular row and column of the grid. For example, the call puzzle.markSpot(1, 2) should fill the spot in row 1 and column 2. In addition, it should have a toString method that returns a String representation of the puzzle, including column and row constraints. For example, if puzzle represents the above puzzle (with the single marked spot), the call System.out.println(puzzle) would display:
For a person, solving a Nonogrid puzzle requires complex and careful logical reasoning. However, it turns out that even the most challenging Nonogrid puzzles can be easily solved by a computer using recursive backtracking. For the second part of this assignment, you are to implement a method that uses recursive backtracking to solve the Nonogrid puzzle. In pseudocode:
The trickiest part of this task will be testing to see whether a partial row or column meets the corresponding constraints. For example, in a 5x5 puzzle, the partial row consisting of two blanks followed by two filled spots meets the constraint "3" but not "3 1" or "4".