Sliding-block Puzzle Solver Project

Background

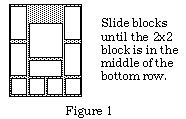
Those of you who spend much time in toy stores may be familiar with "sliding-block" puzzles. They consist of a number of rectangular blocks in a tray; the problem is to slide the pieces without lifting any out of the tray, until achieving a certain configuration. An example (from Winning Ways, E.R. Berlekamp et al., Academic Press, 1982) is shown in Figure 1.

Problem

Write a program named Solver.java that produces a solution to a sliding-block puzzle (if a solution exists) in as little execution time as possible. Your program need not produce the shortest possible sequence of moves. Input to your program will come from the command line and from files named there:

• An optional first argument will be a string whose first two characters are "-o" and whose remaining characters specify information about what instrumentation output the program should produce. (This output is used to identify efficiency bottlenecks in your program. You may choose the format of the argument string.) The string "-ooptions" should cause the program to print all the instrumentation options and the effect of each option. If the "-o" argument is not provided, your program should produce no output beyond that required to display a solution to the puzzle.
• The next argument will name a file that specifies an initial tray configuration. Line 1 of this file will contain two positive integers, the length (number of rows) and width (number of columns) of the tray. Each subsequent line of this file will contain four nonnegative integers describing a block in the tray: the length and width of the block (both greater than 0), and the row and column of the upper left corner of the block. (The upper left corner of the tray is row 0, column 0.) Blocks are indistinguishable except for their size, and may appear in any order in this file. Thus the tray depicted in Figure 1 might be represented in the file as follows:

  	5 4
  	2 1 0 0
  	2 1 0 3
  	2 1 2 0
  	2 1 2 3
  	2 2 1 1
  	1 2 3 1
  	1 1 4 0
  	1 1 4 1
  	1 1 4 2
  	1 1 4 3
  

• The last argument will be the name of a file that specifies a desired final or goal configuration. This file is similar in format to the initial configuration file. Each line of this file contains four nonnegative integers: the length and width of the block (both greater than 0), and the desired position of the upper left corner of the block. This file will not necessarily contain entries for all blocks in the tray. Blocks may appear in any order in this file.
  The goal configuration mentioned in Figure 1 is represented by the single line

  	2 2 3 1
  

  If there were more than one 2-by-2 block in the initial configuration, the one-line goal would specify the position of any of the 2-by-2 blocks.
  
  Figure 2 shows a goal configuration in which three of the 1-by-1 blocks have a specified arrangement, along with the corresponding goal file. Again, if there are more than three 1-by-1 blocks in the initial configuration, it doesn't matter which three of them end up in the specified goal positions.

  goal configuration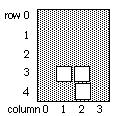	goal file 1 1 3 1 1 1 4 2 1 1 3 2
  Figure 2

Thus your program would be run with the UNIX command

    java Solver [-oinfo] initialConfigFile goalConfigFile

where the -o argument is optional, info is the instrumentation information you supply, and initialConfigFile and goalConfigFile name the files containing the initial block configuration and the goal configuration respectively.

A solution to the puzzle will represent a sequence of position changes of blocks that, when starting with the specified initial configuration, ends up with blocks in the positions specified in the goal. The only legal moves are those that slide a block horizontally or vertically—not both—into adjacent empty space. Blocks may only be moved an integer number of spaces, and either the row or the column will be the same in the start position as in the end position for each move. (It's not legal to rotate the tray of blocks.)

Your program should produce a line of output for each block move that leads directly to a solution. Each such line will contain four integers: the starting row and column of the upper left corner of the moving block, followed by the upper left corner's updated coordinates. Example output appears below; the indicated moves, applied to the starting configuration of Figure 1, achieve the goal in Figure 2. (The annotations would not appear in the solution output.)

If your program, run with instrumentation output disabled, finds a solution to the puzzle, it should exit normally after producing only output as just described, that is, the lines representing block moves that solve the puzzle. In particular, if the initial configuration satisfies the goal, your program should exit normally after producing no output. If your program cannot find a solution to the puzzle, it should exit with the call

	System.exit(1);

again after producing no output.

You should check that command-line arguments are correctly specified, but you may assume that the initial and goal configuration files are free of errors. You may also assume that the length and width of a tray are no larger than 256.

Time/space tradeoffs

Basically, your program will search the tree of possible move sequences to find a solution to the puzzle. It will implement several operations; questions you are to consider in your program design include those outlined below.

• The program will generate moves possible from a given configuration. This will involve examination either of the blocks in the tray or of the empty space in the tray. Should the tray be stored as a list of blocks/empty spaces to optimize move generation, or should the locations in the tray be represented explicitly? If the former, should blocks/spaces in the list be sorted?
• Prior to each move, the program must check whether the desired configuration has been achieved. What tray representation optimizes this operation? If this representation is incompatible with implementations that optimize move generation, how should the conflict be resolved?
• Once it has a collection of possible next moves, the program will choose one to examine next. Should the tree of possible move sequences be processed depth first, breadth first, or some other way?
• Should block moves of more than one space be considered? Why or why not?
• The program needs to make and unmake moves. Again, a representation that optimizes these operations may not be so good for others. Determine how to evaluate tradeoffs among representations.
• The program must detect configurations that have previously been seen in order to avoid infinite cycling. Hashing is a good technique to apply here. What's a good hash function for configurations? The default limits for Java memory allocation may limit the maximum number of configurations that the table can contain. How can this constraint be accommodated, and what effect does it have on other operations?

Some of these questions can be answered with careful analysis. Others require empirical evidence. Incorporate in your program sufficient output information (governed by instrumentation options) to provide this evidence. Discuss your answers to all these questions in your README file (see below).

Miscellaneous requirements

The amount of space your program needs is not an important consideration, except that your program has to fit in the default allocation of memory provided on the workstations in the class lab room. An experiment we recommend is to determine how many configurations you can add to a hash table before you run out of memory. (The blocks in the puzzle described in Figure 1 may be moved into 65880 different configurations. 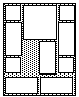The blocks in the diagram below may be moved into 109260 different configurations.)
    

You are to include a isOK method with the class or classes that represents the tray, and provide among your instrumentation options a way to call it. The isOK method should check your tray for consistency, and throw IllegalStateException with an informative message if it finds a problem. When the appropriate instrumentation option is enabled, a call to isOK should accompany each block move.

Organize your program into classes that allow easy substitution of efficient code for inefficient code or of one algorithm for another (e.g. depth-first move processing for breadth-first) in each area. Use straightforward algorithms where possible. Your methods should not be overly long, complex, or repetitive. All data fields and methods within each class must have the proper public/private/protected/package qualifier. In particular, you are not allowed to make things public that would let a user corrupt your data structures (even if none of your own code would do this).

Your code should display good documentation and style. Provide an overview comment with each class that describes the abstract object and any invariants on the abstract object state (e.g. "A Counter represents a mutable, non-negative, non-decreasing integer counter."). Accompany each method with descriptions of its preconditions and effects or return value. When throwing exceptions, supply informative messages. Give your variables and methods informative names that conform to conventions used earlier this semester (class names capitalized, names of constants in all upper case, and names of data members uncapitalized). Indent your code appropriately.

The README file

A substantial part of the credit for this project comes from the README submitted with your program code. This file should include the information listed below, answering all the questions in each category.

• An explanation of how you split the work for this assignment between members of your partnership if you didn't work alone, and why you split it this way. Also indicate the number of points that should be awarded to each partner if you were to distribute 10 extra bonus points for your project between members of your partnership, and explain the division briefly.
• A description of the overall organization of your program—algorithms and data structures—that lists operations on blocks, trays, and the collection of trays seen earlier in the solution search. Diagrams will be useful here to show the correspondence between an abstract tray and your tray implementation. This description should contain enough detail for one of your classmates to understand clearly how the corresponding code would work.
• A description of any other files you're submitting.
• An explanation of how you addressed efficiency concerns in your program:
  • What alternatives did you consider?
  • Why did you accept or reject them? (In particular, you should explain each choice of an array or vector over a linked list and vice-versa, and each choice of a sorted array or vector over an unsorted array vector and vice-versa.)
  • How much memory do your data structures consume when processing typical examples? (Give actual numbers derived from internally instrumenting your program, not big-Oh or big-theta estimates.)
  • How fast do your algorithms work on those examples? (Again, provide actual numbers rather than estimates.)
  • In retrospect, what bad choices did you make and how would you have made them differently?
  • If you were to make one more improvement to speed up the program, what would it be, and what is your evidence for expecting a significant speedup?
  Again, your descriptions of data structures and algorithms, both those that you have implemented and those you have rejected, should contain enough detail for one of your classmates to understand how the corresponding code would work. You should defend every instance where you perform an operation more slowly than the theoretical optimum.
• A description of your instrumentation output facility, how to enable it, and how the output helps you to identify efficiency bottlenecks in your program.

In general, comments in your code will describe information specific to the corresponding class, while the README file contains information that relates classes and describes and provides rationale for design and implementation decisions. However, your README file should be written to be read on its own without a copy of the program code at hand, so there may be some information duplicated in writeup and code.

We encourage you to build the README file as you design and develop your program rather than putting it off until the end.

How your program will be graded

This project will earn up to 120 points, allocated 80 for the program and 40 for the writeup. These points will be scaled to half your project grade. Grading will proceed as follows.

1. Your writeup will be examined for information about your tray data structure, and your isOK method for the tray will be evaluated.
2. Your program will be compiled using the command

   	javac -O Solver.java
   

   If it fails to compile, you get no more program points. The "-O" (minus-Oh) option turns on optimization, and should be used for production runs. For debugging, use Eclipse.
3. Your program will be run, using the command

   	java Solver initialConfigFile goalConfigFile
   

   on a selection of simple puzzles. (These puzzles are online in the directory easy.) You must correctly solve almost all of these puzzles, using under two minutes of execution time for each puzzle, to earn more than 50 program points. (You are of course not allowed to "hard-code" solutions to these puzzles into your program.)
4. Your program will then be run, again using the command

   	java Solver initialConfigFile goalConfigFile
   

   on a selection of difficult puzzles (online in the directory hard), using a lightly loaded workstation configured the same as the workstations in the class lab room. Each one you solve in under two minutes of execution time earns you 3 more points, up to a maximum of 80. Note that we will not be supplying arguments to the Java interpreter that modify the default memory allocation or the default maximum size of the system stack.
5. Stylistic and organizational attributes of your program will then be evaluated to complete your program score. These include information supplied in comments and variable names, formatting and use of white space, organization, a correct isOK method for the tray, and appropriateness of instrumentation output. We will assign a percentage score to these aspects of your code; 100% means no flaws, 90% means minor flaws, and so on. Your program score is the product of your correctness score (from steps 1 through 4) and the style percentage.
6. Your writeup will be evaluated separately to produce the remaining points of your project score.

Miscellaneous information

As with project 2, there will be frequent progress reports and high-level design discussion for homework. The typical solution to this project is around 1000 lines, and many students find they have to rewrite sections of code to satisfy the efficiency constraints. Start planning soon.

In the proj3 directory is a Checker program that checks whether a given sequence of moves solves a given puzzle. The program takes two arguments, an initial configuration and a goal configuration in the same format as those for Solver.java. It also takes a sequence of moves, in the format to be produced by Solver.java, as standard input. Its output indicates whether the moves solve the puzzle, and if not, why not. On a UNIX system, you might run the program as follows:

	java Solver init goal | java Checker init goal

("Init" and "goal" stand for names of files containing the initial and goal configurations, respectively.)

To use the program, copy the files Checker.class and TrayVerifier.class from the proj3 directory. Warning: It doesn't check for extraneous junk characters on a line, instead giving a rather difficult-to-understand error message involving the inability to move.